作为成熟的生物医学科研人，必然是做实验、写论文、做生信分析……样样手到擒来！今天，我们再来接着解读PCA图~
一、定义和用途
定义：PCA（主成分分析图）是以“降维"为核心，把多指标的数据用少数几个综合指标（主成分）替代，还原数据最本质特征的数据处理方式，用于展示多元数据的主要模式和结构。
用途：
常用于疾病危险因素分析、肠道菌群聚类分析、肿瘤亚群之间的进化关系分析等。
l 确定主成分的数量：通常来说，保留前几个主成分就足够解释原始数据的大部分变异。
l 异常值检测：通过观察PCA图中样本的分布情况，可以发现是否存在异常值。如果某个样本在各个主成分上的得分都明显偏离其他样本，则表示该样本为异常值。聚类分析：通过观察PCA图中样本的分布情况，将相似的样本归为同一类，不相似的样本归为不同类。
l 预测分析：如果已知某些样本属于某一类或具有某一标签，就可以在PCA图中找到这些样本的位置，并预测新样本的分类或标签。
二、PCA图怎么看（案例解读）
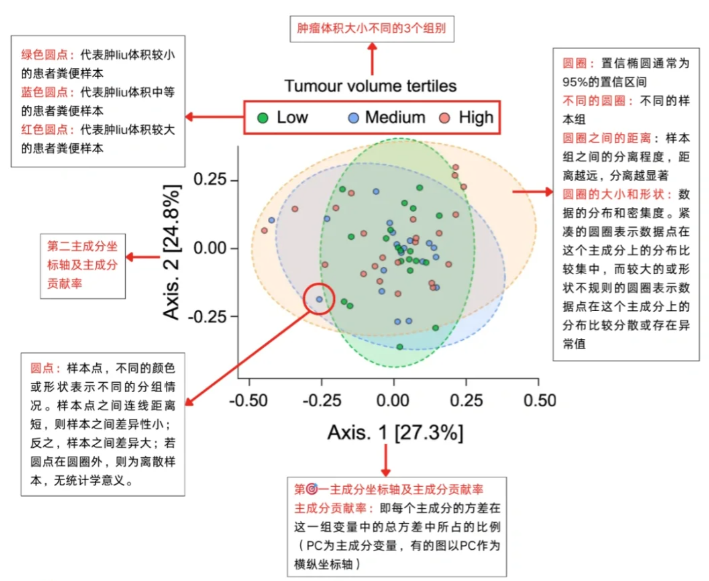
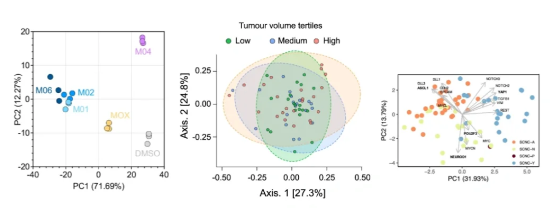
为了测试肿瘤体积大的患者是否系统性地表现出其微生物群的变化，研究者使用Bray-Curtis指数测量了整个队列的β多样性。主成分分析（PCA）显示这些患者的β多样性无显著差异。
三、相关疑问和解答
1.什么是主成分？
主成分就是原始变量的线性组合。
第一主成分对应第一坐标轴，表示了原始数据中多个变量通过某种变换得到的新变量的变化范围，能够最大程度解释数据中方差的线性组合。
第二主成分则对应第二坐标轴，代表了第二个新变量的变化范围，能够最大程度解释数据中的方差。
2.PCA分析有哪些注意事项？
l 当我们遇到非线性的或高阶相关的变量关系时，就无法通过PCA分析发挥数据降维的作用。
l 当我们遇到两个变量的数值尺度相差较大时，必须先进行标准化处理，确保变量之间的数值尺度相同，才能进行PCA分析。
l 当我们进行PCA分析时，需要假设变量服从高斯分布，如果变量不服从高斯分布（例如均匀分布时），则会发生尺度缩放与旋转。
3.PCA图有哪些衍生类型？
（1）PCA散点图
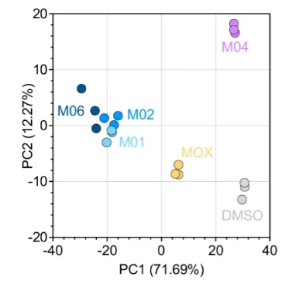
（2）PCA双标图
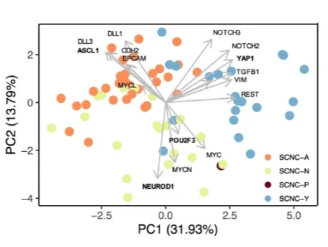
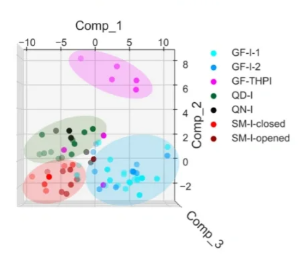
（3）PCA三维图
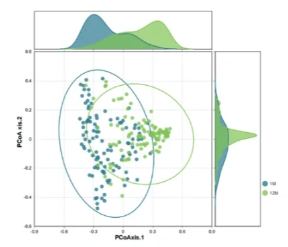
（4）PCA山脊图
文章推荐
业务咨询
业务咨询专线：133 7682 0615
Email:lxyjy@wie-biotech.com
